Hello,
great progress in the integration of the gmsh 2D to the rest of the meshing tools of MESH as now I can use the GMSH 2D which respects the 1D discretization of the solid.
nevertheless, I might be missing something, or this is ‘still on work’, as I am not able to use it a compound of solids.
here is a simple example of this:
exampleGMSH.hdf (843,2 KB)
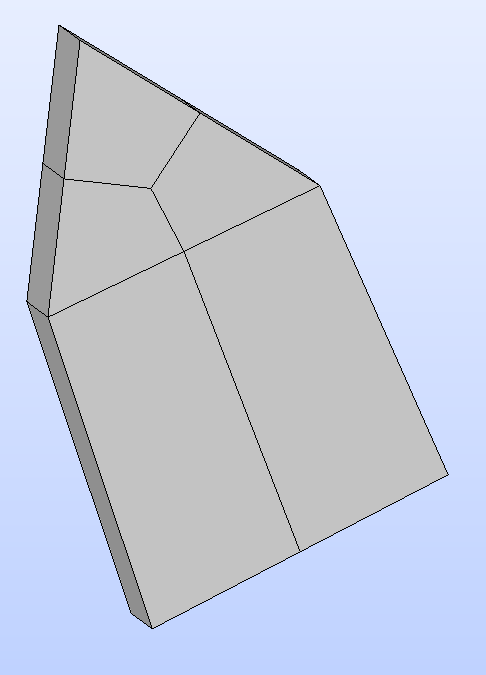
here we have a compound of two solids, a triangle prism, and an hexagon which share one face.
in a ‘normal’ workflow of salome meshing, one can:
- create a mesh of the compound
- create a submesh of all edges together
- create a submesh over ONE of the triangular faces of the triangle prism
- create a submesh over all quadrangle faces of the compound (including quad faces of the triangular prism and all faces of the hexagon)
- create a submesh of the triangle prism with extrusion 3D
- create a submesh of the hexagon with hexagon I,j,k
this creates a conformal mesh with triangular prism and hexagon elements on the mesh.
if now we change the step 3. and select gmsh 2D/quasi structured quad when computing the mesh, it will fail.
now if we take a body that has only the triangular prism and we ‘repeat’ the workflow so:
- create a mesh
- create submesh of the body extrusion 3D
- create submesh of ONE face with GMSH 2D quasi structured quad
- create submesh of all edges
the mesh will be success and now (in difference to previous salome versions) the quasi structured quad WILL respect the discretization of the edges.
so, in theory the meshing of the compound being conformal should be possible. is this a bug? or I am doing something wrong?
EDIT: my bad it looks that still does not work in any case
Hello ,
The problem seems to come from the 1D Hypotheses:
- A 1D discretization is applied on all edges (including those delimiting triangles)
- We want to use gmsh2d with Quasi-strucutured which requires a 1D discretization different from the one previously imposed.
This creates a conflict which does not allow gmsh2d to generate a quadrangular surface mesh.
By pre-cutting the geometry into blocks of 6 faces each as shown here
,
the mesh is correctly generated with gmsh2D for the triangles and Quadrangle Mapping for the rest.
There is no conflict in this case because the 1D discretization is consistent everywhere.
Please find the new hdf file here exampleGMSH_MK.hdf (3,4 Mo)
Mohamed
Hello mohamed,
thanks for your answer,
I understood what you meant with - We want to use gmsh2d with Quasi-strucutured which requires a 1D discretization different from the one previously imposed.
and that with the new modified geometry it works,but I don’t understand what makes or not work in one or other geometry, I mean how it can the conflict be removed while fixing the 1D?.
with you approach of ‘cutting the triangular faces’ it actually becomes 100% meshable with simple quadrangulate (and even the hexa meshing easily done with the hexahedron ) and would give an excellent result. as in your other post about the heat exchanger Hexahedral mesh help - #3 by M.KARADANIZ-Phimeca you are dividing the geometry into blocks and applying quasi-structured quad from gmsh. but this does not have a lot of sens, as for a block divided geometry one can simply use quadrangle mapping and get a better mesh quality. what I was looking to use this algorithm is to mesh non-quadrangle faced prisms while respecting the 1D discretization to have a conformal mesh with the rest. to have unstructured hex meshes such as is done in cubit with paving (2D)+sweep(3D) do in salome with quasi-struc quad (2D)+extrusion (3D) so dividing the prism into blocks removes any benefit from the use of unstructured meshes…
Alright . The subdivision into blocks was just a way to illustrate the origin of the problem.
gmsh2D with quasi-strucutured algorithm embeds a 1D discretization, which in this case comes in conflict with the global 1D you are trying to assign .
For other 2D algorithms where 1D discretization is explicitily defined in Mesh module, you can define a discretization priority between conflicting 1D hypthoses.
This is not the case here because ,as said earlier, the quasi-structured algorithm embeds implicitly a 1D algorithm.
Mohamed
Hi,
a workaround is to:
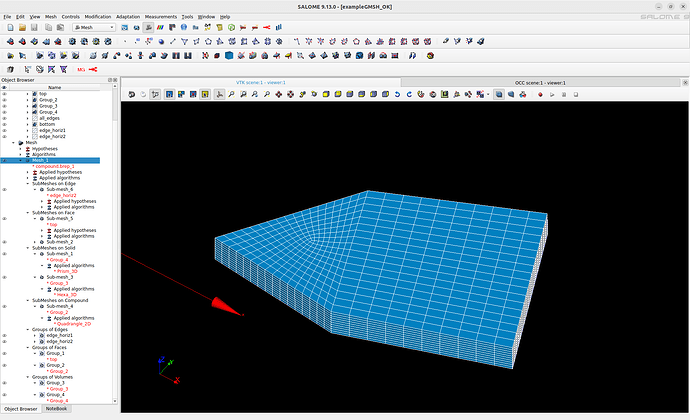
- mesh the desired face with quasi-structured quad, without assigning numbers of segments on edges.
- then, get the number of segments on the edge on which you want to get a quadrangle mesh (for instance with mesh information on edge_horiz1 in exampleGMSH_OK.hdf),
- then set this number to opposite edges (cf Sub-mesh_6 on edge_horiz2).
This may be automatized in a python script.
Christophe
Hello Christophe,
thanks for your input, I see what you mean (I mean the logic behind) and could implemented easily but this stills makes the 2D ‘over’ the 1D where I was looking the other way around (I mean that the 2D follows the 1D) as the classic approach of salome. it is sad as this is a great algorithm that would be awsome to have available to combine with all the rest (as with this work around we can not use specific 1D algorithms,etc.). for the moment, the most ‘near’ this approach, is in Gmsh2D to use the frontal deleurian for quads algo +blossom + recombine all triangular meshes, but this gives by far a lower quality mesh (also to notice, if we use in the 2D recombination algorithm simple full-quad or blossom full-quad the mesh will fail). for simple prisms the procedure to cut them automatically in the geometry level and do a quadrangle: mapping is doable, I have a script that does it automatically, but the quasi-structured quad would had allow for much more complex geometries of prisms to mesh with fully hexas.
regards,
franco
Hello Mohamed,
I didnt saw your answer before the one from christophe, my excuses. I understand and IMO, gmsh should be divided into gmsh 1D2D (only quasi-struc quad and also from my testings looks like the 2D recombination algorithms full-quads) and gmsh2D (asthe case with other algorithms, such as netgen, projection, import elements…) would be way more clearer, as some meshers from gmsh respect an external 1D and others no. hope that at one moment, it will be possible to remove the embebed 1D discretization of the quasi-struc quad.
regards,
franco