Dear all,
I am trying to build a simple p, q torus knot with some thickness; however I am facing some challenges to extrude a disk along the path on the torus. I saw some examples along an helix working fine but here it fails.
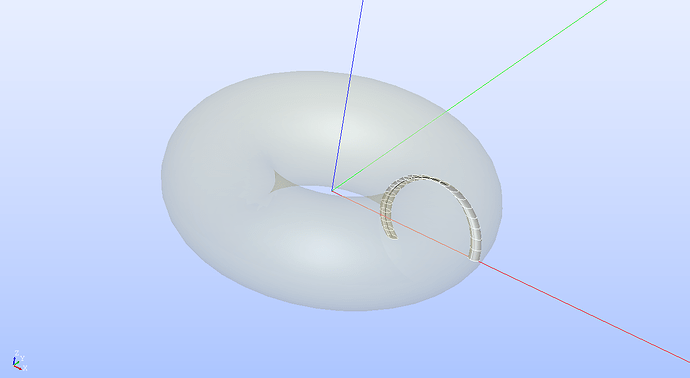
Maybe I am not using correctly the “extrusion along path” feature. I am providing the code below to generate the case study and a screenshot of a fraction of the path:
# p, q torus knot
import salome
salome.salome_init_without_session()
import GEOM
from salome.geom import geomBuilder
geompy = geomBuilder.New()
import math
import SALOMEDS
import numpy as np
# Parameters of the torus
b, c, a = 0.1, 2, 1
p, q = 1, 12
# GEOM.Polyline
# GEOM.Bezier (Not working)
# GEOM.Interpolation
# create a polyline using parametric definition of the basic points
nbp = 20
ad = 0.1
pqtorus = geompy.MakeCurveParametric("(c+a*cos(q*t))*cos(p*t)", "(c+a*cos(q*t))*sin(p*t)", "a*sin(q*t)", 0., ad * np.pi, nbp, GEOM.Polyline, theNewMethod=True)
# Initial point
t_0 = 0
theta_0 = p*t_0
phi_0 = q*t_0
x_0 = (c+a*np.cos(phi_0))*np.cos(theta_0)
y_0 = (c+a*np.cos(phi_0))*np.sin(theta_0)
z_0 = a*np.sin(phi_0)
p_0 = geompy.MakeVertex(x_0, y_0, z_0)
# Normalized tangent vector
t_x = -p*(c+a*np.cos(phi_0))*np.sin(theta_0)-q*a*np.sin(phi_0)*np.cos(theta_0)
t_y = p*(c+a*np.cos(phi_0))*np.cos(theta_0)-q*a*np.sin(phi_0)*np.sin(theta_0)
t_z = q*a*np.cos(phi_0)
t_n = np.sqrt(t_x**2 + t_y**2 + t_z**2)
t_nx = t_x / t_n
t_ny = t_y / t_n
t_nz = t_z / t_n
p_1 = geompy.MakeVertex(x_0+t_nx, y_0+t_ny, z_0+t_nz)
vt = geompy.MakeVector(p_0, p_1)
# Normal vector
n_x = np.cos(theta_0)*np.cos(phi_0)
n_y = np.sin(theta_0)*np.cos(phi_0)
n_z = np.sin(phi_0)
p_2 = geompy.MakeVertex(x_0+n_x, y_0+n_y, z_0+n_z)
vn = geompy.MakeVector(p_0, p_2)
# Binormal vector
b_x = t_ny*n_z-t_nz*n_y
b_y = -(t_nx*n_z-t_nz*n_x)
b_z = t_nx*n_y-t_ny*n_x
p_3 = geompy.MakeVertex(x_0+b_x, y_0+b_y, z_0+b_z)
vb = geompy.MakeVector(p_0, p_3)
# Local coordinate system (lcs)
lcs = geompy.MakeMarkerPntTwoVec(p_0, vt, vn)
# Create a disk at the origin
disk = geompy.MakeDiskPntVecR(p_0, vt, b)
# Supporting torus
torus = geompy.MakeTorusRR(c, a)
# Extrusion
cable = geompy.MakePipe(disk, pqtorus, IsGenerateGroups=False)
#cable = geompy.MakePipeBiNormalAlongVector(disk, pqtorus, vb, IsGenerateGroups=False)
# add objects in the study
torus_id = geompy.addToStudy(torus, "torus")
torus.SetColor(SALOMEDS.Color(1,1,0.5))
pqtorus_id = geompy.addToStudy(pqtorus, "pqtorus")
pqtorus.SetColor(SALOMEDS.Color(0,0,0))
geompy.addToStudy(vt, "tangent: t")
geompy.addToStudy(vn, "normal: n")
geompy.addToStudy(vb, "binormal: b")
geompy.addToStudy(lcs, "LCS")
geompy.addToStudy(disk, "disk")
geompy.addToStudy(cable, "cable")
# Open a study and the geomtry module before running the script
gg = salome.ImportComponentGUI("GEOM")
gg.createAndDisplayGO(torus_id)
gg.setDisplayMode(torus_id, 1)
gg.setTransparency(torus_id,0.75)
gg.createAndDisplayGO(pqtorus_id)
gg.setDisplayMode(pqtorus_id, 1)
Best regards,
Frederic